Swinburne Commons
MathsCasts
A daily podcast
Good podcast? Give it some love!
Swinburne Commons
MathsCastsEpisodes
Swinburne Commons
MathsCasts
A daily podcast
Good podcast? Give it some love!
Rate Podcast
Episodes of MathsCasts
Mark All
Search Episodes...
Introduces the idea of half-range Fourier series and addresses the question of why we use them.
Deals with the details of calculating Fourier series coefficients for a function.
We solve simultaneously the equations of a plane and a cone and show that the intersections are circles, parabolas, ellipses, hyperbolas, straight lines or just the origin.
Demonstrates that symmetry of functions helps us to shorten the calculation of the integrals needed for the Fourier coefficients.
Example of solving a set of simultaneous linear 1st order ODE's with Laplace transforms (MathsCasts)
Standard pair of linear, coupled 1st order DE's solved by Laplace transform method.
Sketch of y =(x+1)^3-2.
Demonstration of using Laplace transform to solve a 2nd order, linear, non-homogeneous, constant coefficient DE with boundary conditions and with right hand side appearing in the CF.
Sketch of y = 2(x+2)(x-2)(x+3).
Demonstration of using Laplace transform to solve a 2nd order, linear, non-homogeneous, constant coefficient DE with boundary conditions and with right hand side appearing in the CF.
Example of solving a set of simultaneous linear 1st order ODE's with Laplace transforms (MathsCasts)
Standard pair of linear, coupled 1st order DE's solved by Laplace transform method.
Brief and simple introduction to the first shift theorem for Laplace transforms.
We solve a non-homogeneous 2nd order constant coefficient ODE with boundary conditions using the Laplace transform method. A check is applied to the solution. The process of solving is then repeated with a deliberate error and it is demonstrate
Brief introduction to why we use Laplace transforms, with mention of tables.
We solve a non-homogeneous 2nd order constant coefficient ODE with boundary conditions using the Laplace transform method. A check is applied to the solution. The process of solving is then repeated with a deliberate error and it is demonstrate
Detailed discussion of using Laplace transform to solve a 1st order ODE.
Sketch of y =(x+1)^3-2.
Sketch of y = 2(x+2)(x-2)(x+3).
In this recording we look at an example of differentiation using the inverse function rule.
Sketch of y = 2(x+1)^2-3.
In this recording we look at an example of differentiation using the inverse function rule.
The quotient rule for differentiation is proved from first principles.
The quotient rule for differentiation is proved from first principles.
Integration by parts is used to integrate the product of two polynomials.
Demonstrates that symmetry of functions helps us to shorten the calculation of the integrals needed for the Fourier coefficients.
The chain rule for differentiation is proved from first principles. Use is made of the small difference formula, which is discussed first.
Join Podchaser to...
- Rate podcasts and episodes
- Follow podcasts and creators
- Create podcast and episode lists
- & much more
Unlock more with Podchaser Pro
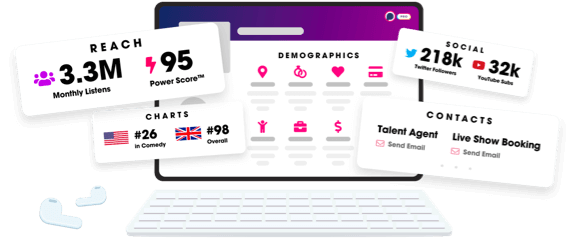
- Audience Insights
- Contact Information
- Demographics
- Charts
- Sponsor History
- and More!
- Account
- Register
- Log In
- Find Friends
- Resources
- Help Center
- Blog
- API
Podchaser is the ultimate destination for podcast data, search, and discovery. Learn More
- © 2024 Podchaser, Inc.
- Privacy Policy
- Terms of Service
- Contact Us