Episodes of MathsCasts
Mark All
Search Episodes...
In this recording use the inverse function rule for differentiation to find the derivate of the inverse sine of x. This example includes discussion of the importance of looking at the graph of such a function, to see whether it is increasing or
We solve simultaneously the equations of a plane and a cone and show that the intersections are circles, parabolas, ellipses, hyperbolas, straight lines or just the origin.
We demonstrate that the equation y = 1/x transforms to standard form for an hyperbola under rotation of the coordinate axes by 45 degrees.
Two examples of simplifying expressions of the form trig(inverse trig), using right angled triangles. The result is in algebraic form without trig functions
We prove some results on horizontal shifts applied to the sin and cos functions.
We prove that cos(-x) = cos(x) and sin(-x) = - sin(x|)
We prove the formula for sin(A-B) using right-angled triangles then we show how the corresponding formulae for cos(A-B) and sin and cos of A+B can be deduced as a result.
We look at a second example involving combinations of direction, one of which is none of north, south, east or west.
We introduce the points of the compass and solve a simple example using distances and basic directions (N,S,E,W) to find resulting distance and angle.
Several examples are given of rewriting composite circular functions, where the inner function is an inverse trigonometric function, as an algebraic function in terms of x.
Explains how the equations of two parallel planes are related - then solves a problem where a plane parallel to a given plane, passing through a point, is to be found.
This recording looks at how to identify the nature of the region in the complex plane that satisfies |z-z0|=r. This is then illustrated further with a specific example.
An explanation is given of the general visual interpretation of polar coordinates. An example of then given of choosing different angles, evaluating 'r' at each of these angles and then plotting and joining the resulting points by hand.
This recording explains the relationship between Polar and Cartesian coordinates of a 2D curve. An example is then given of converting a polar equation into Cartesian form and an example is given of converting a Cartesian equation into polar fo
Considering a line written in scalar parametric form and a plane written in form ax + by + cz = d, three examples investigate if and where line and plane intersect: in one point; the line lies on the plane; or line and plane are parallel and ne
This recording starts by showing how the equation of a plane relates to its normal vector. An example is then done to show how this allows us to find the equation of a plane, provided we also know a point on the plane.
Given a point and a line on a plane, we find the equation of the plane.A second point on the plane is identified, and hence a vector on the plane. A normal vector to the plane is calculated using the vector product.The equation of the plane is
This screencast gives two examples of converting the parametric equations of 2D curves into Cartesian equations, and includes a discussion on the importance of considering any restrictions of the domain of the resulting Cartesian equations in e
This recording starts by giving the general formula for calculating the angle between two planes by finding the angle between their normal vectors. An example is then given to illustrate this.
This screencast gives an example of sketching vertical and horizontal cross-sections of a surface and hence producing a final sketch of the resulting 3D surface (which is an elliptical hyperboloid of two sheets)
Example where equation of a plane and scalar parametric equations of a line are given. To find the angle between the line and the plane, the equations of the line are converted to vector form, the angle between the line and the normal vector to
An example where the gradient of a surface is found depending on the angle alpha, and then the maximum gradient is calculated.
Application of vectors to the example of finding the equation of a plane through three points by first determining two vectors on the plane, then using the cross product to determine a normal vector to the plane, then using the normal vector an
This screencast gives explanation of two rules for finding unknown angles and/ or lengths of sides in any triangle: the Sine Rule and the Cosine Rule. Examples are then given to show how to apply each rule in practice.
The screencast begins by outlining the rules for finding angles in a right-angled triangle given the lengths of two of its sides. Examples are then given of applying these rules: both to finding an angle given the length of two sides in a right
Join Podchaser to...
- Rate podcasts and episodes
- Follow podcasts and creators
- Create podcast and episode lists
- & much more
Unlock more with Podchaser Pro
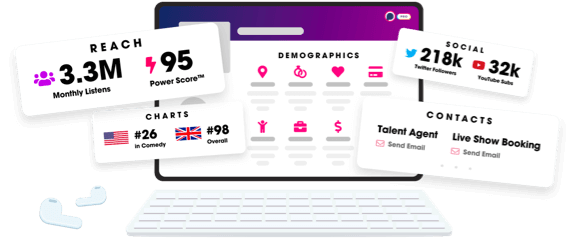
- Audience Insights
- Contact Information
- Demographics
- Charts
- Sponsor History
- and More!
- Account
- Register
- Log In
- Find Friends
- Resources
- Help Center
- Blog
- API
Podchaser is the ultimate destination for podcast data, search, and discovery. Learn More
- © 2024 Podchaser, Inc.
- Privacy Policy
- Terms of Service
- Contact Us
